Mục lục
I. KIẾN THỨC CƠ BẢN
1. Thế nào là phương pháp chứng minh phản chứng
– Trong nhiều bài toán để chứng minh $\mathrm{B}$ là đúng, người ta chứng minh phủ định của $\mathrm{B}$ là sai.
– Phương pháp chứng minh phản chứng là phương pháp chứng minh gián tiếp, trong đó để chứng tỏ kết luận của bài toán là đúng, ta chứng minh phủ định của kết luận là sai.
Ví dụ:
Để chứng minh AB<CD ta chứng minh rằng AB>CD là sai.
Để chứng minh nếu 2 đường thẳng phân biệt bị cắt bởi đường thẳng thứ ba và tạo ra 2 góc trong cùng phía bù nhau thì 2 đường thẳng đó song song, ta chứng minh nếu 2 đường thẳng đó cắt nhau thì sai.
2. Các bước chứng minh bài toán phản chứng
Bước 1: Phủ định kết luận (giả sử có điều trái với kết luận của bài toán).
Bước 2: Rút ra điều vô lí (từ giả thiết, lập luận dẫn đến điều vô lí, vô lí có thể là trái giả thiết hoặc trái với một điều đúng nào đó, trái với thực tế, trái với kiến thức đã học dẫn đến mâu thuẫn).
Bước 3: Khẳng định kết luận bài toán. Từ mâu thuẫn trên, ta khẳng định điều trái với kết luận bài toán là sai, kết luận của bài toán là đúng.
II. CÁC VÍ DỤ

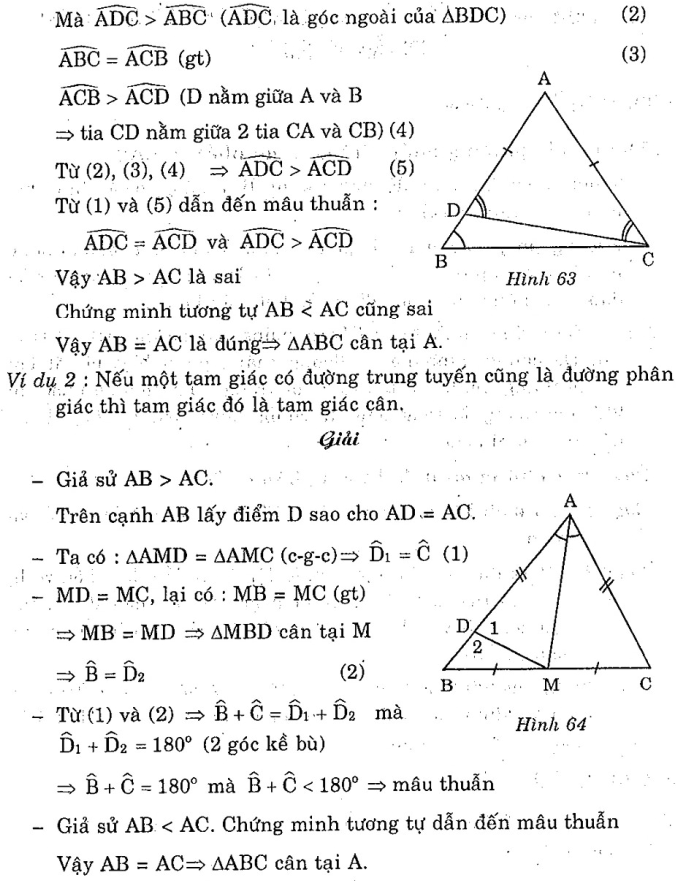
II. BÀI TẬP

