Trật tự các phép toán hay thứ tự thực hiện các phép tính được thực hiện như thế nào cho đúng quy tắc để không bị sai?
Xét một bài toán nhỏ của học sinh dưới đây.
Bài toán: Tính giá trị biểu thức số học sau: 3 + 4 x 2
Lời giải:
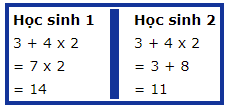
Điều này cho thấy mỗi học sinh hiểu bài toán theo cách khác nhau, kết quả là có hai đáp số. Học sinh 1 thực hiện tính phép cộng đầu tiên, sau đó là phép nhân. Nhưng ngược lại, học sinh 2 thực hiện phép nhân trước, sau đó là phép cộng. Bao giờ thì các phép toán số học cũng có một trật tự nên ta chỉ có thể có một đáp số đúng mà thôi. Chúng ta cần đặt ra các quy tắc theo trình tự để ngăn ngừa khả năng nhầm lẫn. Các nhà toán học đã để lại một trật tự các phép toán làm chuẩn cho sự tính toán khi giải các bài toán số học có nhiều hơn một phép toán.
Quy tắc thực hiện phép tính
- Quy tắc 1: Trước nhất, thực hiện bất kỳ phép toán nào bên trong dấu ngoặc đơn.
- Quy tắc 2: Tiếp theo, thực hiện tất cả các phép nhân và phép chia theo thứ tự từ trái qua phải.
- Quy tắc 3: Cuối cùng, thực hiện tất cả các phép cộng và trừ theo thứ tự từ trái qua phải.
Bài toán trên đã được giải đúng bởi học sinh thứ 2 do bạn đó đã đi theo quy tắc 2 và 3. Chúng ta hãy cùng xem một vài Ví dụ về giải các biểu thức số học có sử dụng các quy tắc này.
Ví dụ 1: Tính giá trị của mỗi biểu thức dựa trên các quy tắc về thứ tự thực hiện các phép toán.
Lời giải:
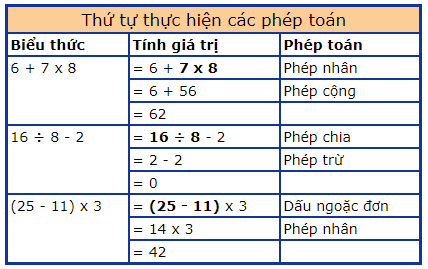
Trong Ví dụ 1, mỗi bài toán chỉ có hai phép tính. Chúng ta hãy xem xét một vài Ví dụ bao hàm nhiều hơn hai phép toán.
Ví dụ 2: Tính giá trị biểu thức 3 + 6 x (5 + 4) ÷ 3 – 7 theo thứ tự thực hiện các phép toán.
Lời giải:

Ví dụ 3: Tính 9 – 5 ÷ (8 – 3) x 2 + 6 bằng cách sử dụng trật tự các phép toán.
Lời giải:

Trong Ví dụ 2 và 3, bạn để ý thấy rằng phép nhân và phép chia được tính từ trái qua phải theo quy tắc 2. Tương tự, phép cộng và phép trừ được tính từ trái qua phải theo quy tắc 3.
Khi hai hoặc nhiều hơn các phép toán xuất hiện phía trong một tập hợp các dấu ngoặc đơn, các phép toán sẽ được tính dựa theo quy tắc 2 và 3. Chúng ta thực hiện điều này trong Ví dụ 4 dưới đây.
Ví dụ 4: Tính 150 ÷ (6 + 3 x 8) – 5 bằng cách sử dụng trật tự các phép toán.
Lời giải:
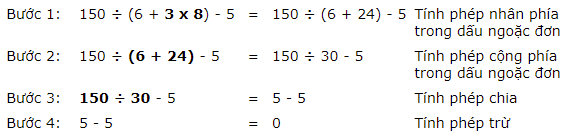
Ví dụ 5: Tính biểu thức số học: $\frac{36-6}{12+3}$
Lời giải: Bài toán này có chứa một dấu phân số (dấu gạch ngang), điều đó có nghĩa là chúng ta phải chia tử số cho mẫu số. Tuy nhiên, trước nhất chúng ta phải thực hiện tất cả các phép tính ở phía bên trên và phía bên dưới dấu phân số trước khi thực hiện phép chia.
Do đó $\frac{36-6}{12+3}=\frac{(36-6)}{(12+3)}$
Tính biểu thức, chúng ta thu được: $\frac{36-6}{12+3}=\frac{(36-6)}{(12+3)}=\frac{30}{15}=2$
Kết luận
Khi tính các biểu thức số học, trật tự thực hiện các phép toán là:
- Làm đơn giản hóa tất cả các phép tính bên trong các dấu ngoặc đơn.
- Thực hiện tất cả các phép nhân và phép chia, từ trái sang phải.
- Thực hiện tất cả các phép cộng và phép trừ từ trái sang phải.
- Nếu bài toán có chứa dấu phân số, thực hiện tất cả các phép tính phía bên trên và bên dưới dấu phân số trước khi đem tử số chia cho mẫu số.
