“Phép chia cho bội” hay còn gọi là “phép chia gấp đôi” là phương pháp được áp dụng cho các số chia và số bị chia có nhiều chữ số, như chia số có 6 (hoặc 7) chữ số cho số có 3 (hoặc 4) chữ số.
Các bước thực hiện phép chia cho bội có thể kéo dài nhưng sẽ giúp học sinh đỡ vất vả và hạn chế được sai sót.
Phương pháp phép chia cho bội vận dụng mối liên hệ rất cơ bản giữa phép chia và phép trừ mà chúng ta đã được học trong các bài trước: “Đáp số của phép chia có thể thu được bằng cách thực hiện phép trừ lặp đi lặp lại”. Nếu bạn vẫn chưa nắm vững điều này, xin xem lại bài học “Mối liên hệ của phép chia với phép trừ“.
Phép chia là phép trừ lặp đi lặp lại nhiều lần. Ở đây ta không đem số bị chia trừ trực tiếp cho số chia mà trừ cho bội số của số chia (mà bội đó vẫn nhỏ hơn số bị chia). Trong phép chia cho bội theo chuẩn, ta đem số bị chia trừ dần cho các bội số chẵn thích hợp của số chia. Bội số này có được bằng cách đem nhân gấp đôi số chia với các số chẵn 2-4-8 và phải đồng thời thỏa mãn 2 điều kiện: vừa là bội số lớn nhất và vừa nhỏ hơn số bị chia.
Ví dụ 1:
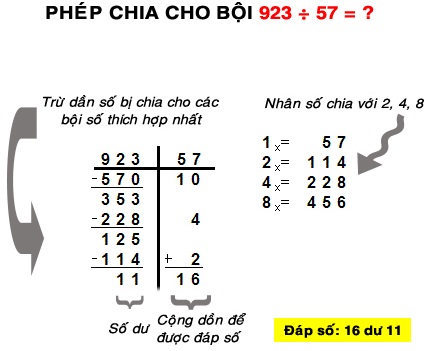
Phương pháp “phép chia cho bội” áp dụng với số chia có 2 chữ số (57) và số bị chia có 3 chữ số (923) gồm các bước dưới đây:
- Nhân đôi số chia (57) ba lần, tức nhân số chia lần lượt với các trị số 2 (lần 2x), 4 (lần 4x), 8 (lần 8x) và:
- Đặt số chia (57) ở góc phần tư thứ nhất và đặt số bị chia (923) ở góc phần tư thứ hai (xem hình).
- Lựa chọn các bội số thích hợp của số chia trong các bội 2x, 4x, 8x và đặt nằm dưới số bị chia (923) sao cho bội này luôn thỏa mãn đồng thời 2 điều kiện: vừa là bội số lớn nhất vừa nhỏ hơn số bị chia.
- Trừ lần lượt số bị chia cho các bội đã lựa chọn ở trên cho đến khi thu được số bị chia mới nhỏ hơn số chia (bội 1x).
- Cộng dồn các bội và số dư nếu có để được đáp số cuối cùng.
- Đáp số của phép chia 923 cho 57 là 16 dư 11.
Ví dụ 2:
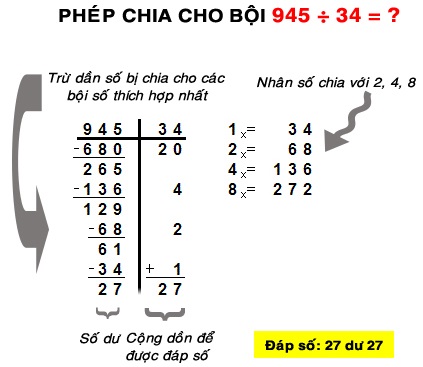
Phương pháp “phép chia cho bội” áp dụng với số chia có 2 chữ số (34) và số bị chia có 3 chữ số (945) gồm các bước dưới đây:
- Nhân đôi số chia (34) ba lần, tức nhân số chia lần lượt với các trị số 2 (lần 2x), 4 (lần 4x), 8 (lần 8x) và:
- Đặt số chia (34) ở góc phần tư thứ nhất và đặt số bị chia (945) ở góc phần tư thứ hai (xem hình).
- Lựa chọn các bội số thích hợp của số chia trong các bội 2x, 4x, 8x và đặt nằm dưới số bị chia (945) sao cho bội này luôn thỏa mãn đồng thời 2 điều kiện: vừa là bội số lớn nhất vừa nhỏ hơn số bị chia.
- Trừ lần lượt số bị chia cho các bội đã lựa chọn ở trên cho đến khi thu được số bị chia mới nhỏ hơn số chia (bội 1x).
- Cộng dồn các bội và số dư nếu có để được đáp số cuối cùng.
- Đáp số của phép chia 945 cho 34 là 27 dư 27.
Ví dụ 3:
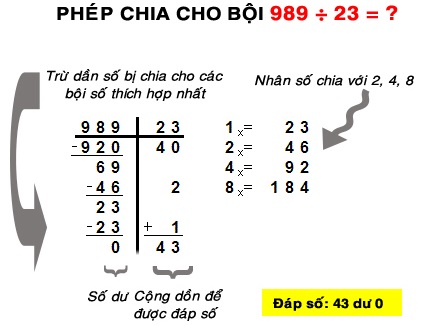
Phương pháp “phép chia cho bội” áp dụng với số chia có 2 chữ số (23) và số bị chia có 3 chữ số (989) gồm các bước dưới đây.
- Nhân đôi số chia (23) ba lần, tức nhân số chia lần lượt với các trị số 2 (lần 2x), 4 (lần 4x), 8 (lần 8x) và:
- Đặt số chia (23) ở góc phần tư thứ nhất và đặt số bị chia (989) ở góc phần tư thứ hai (xem hình).
- Lựa chọn các bội số thích hợp của số chia trong các bội 2x, 4x, 8x và đặt nằm dưới số bị chia (989) sao cho bội này luôn thỏa mãn đồng thời 2 điều kiện: vừa là bội số lớn nhất vừa nhỏ hơn số bị chia.
- Trừ lần lượt số bị chia cho các bội đã lựa chọn ở trên cho đến khi thu được số bị chia mới nhỏ hơn số chia (bội 1x).
- Cộng dồn các bội và số dư nếu có để được đáp số cuối cùng.
- Đáp số của phép chia 989 cho 23 là 43 dư 0.
